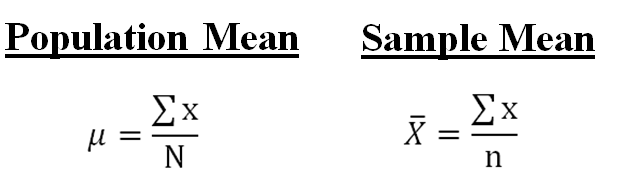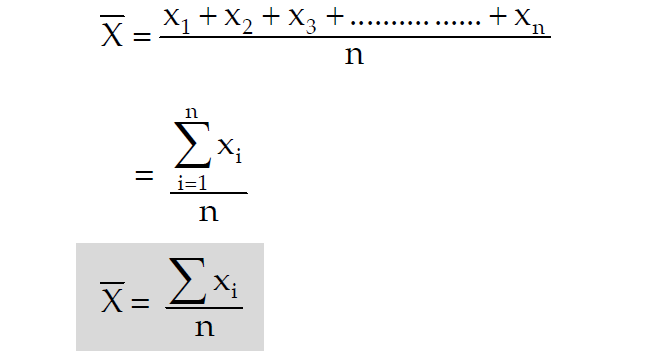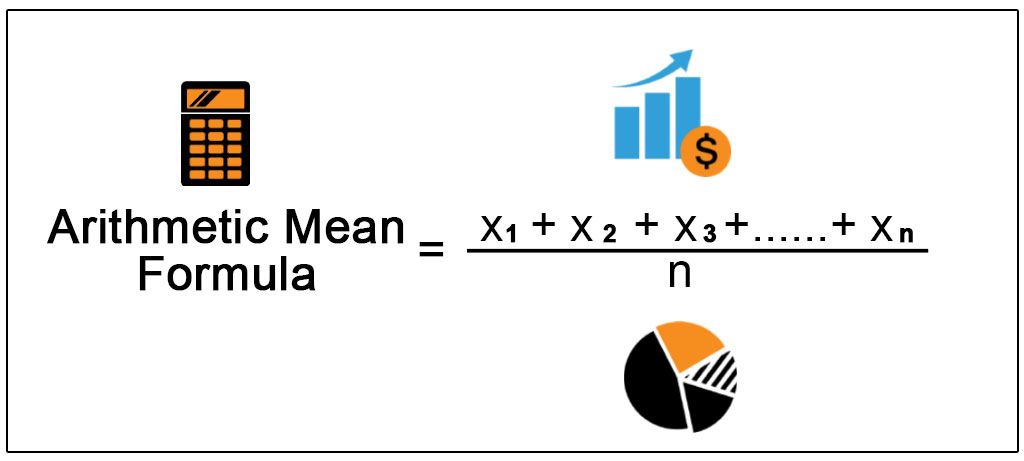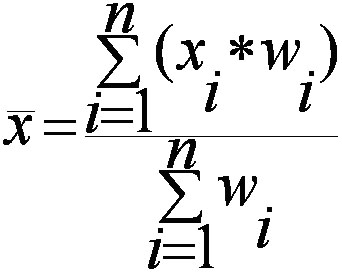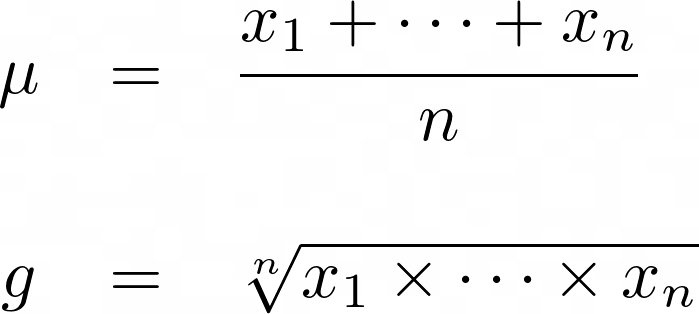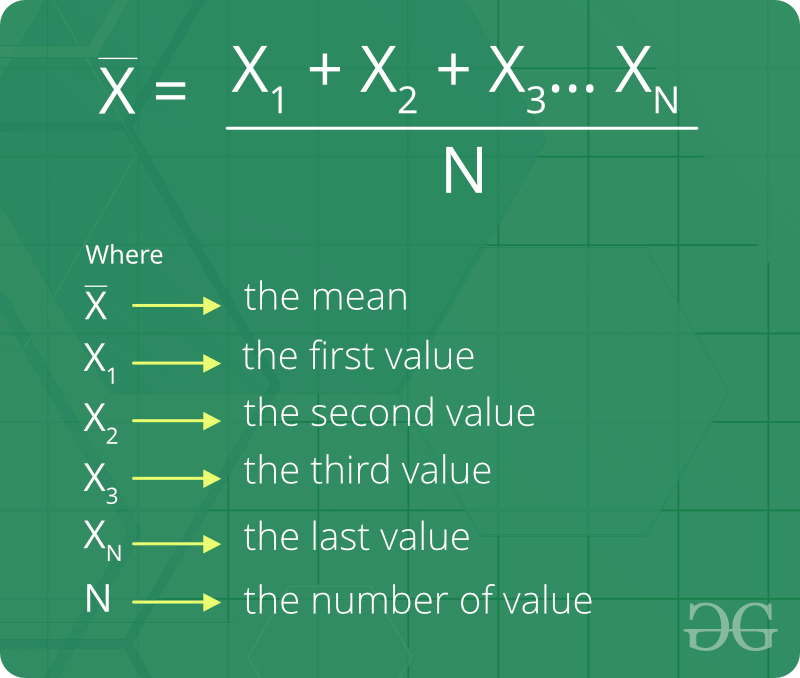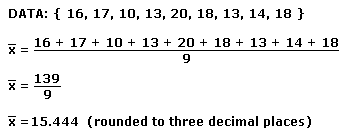Formula Of Arithmetic Mean In Statistics
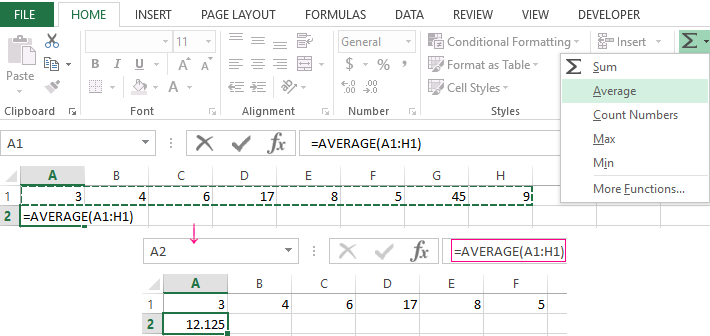
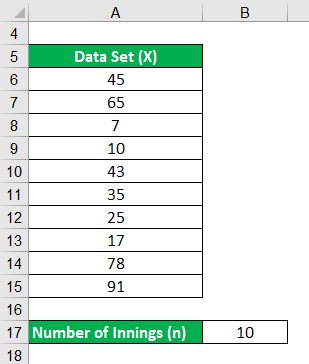
For example find the mean of given values.
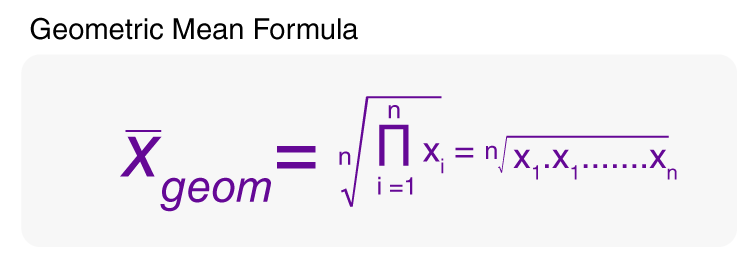
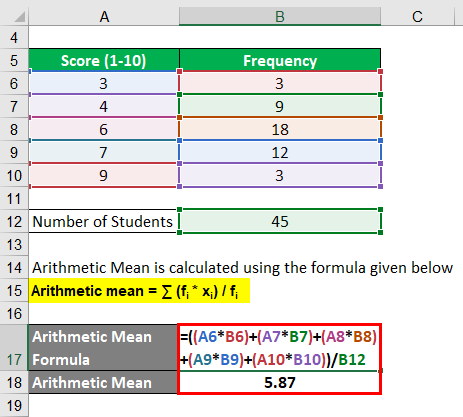
Formula of arithmetic mean in statistics. Lets look at some more. Both formulas have a mathematical symbol that tells us how to make the calculations. In the problem above the mean was a whole number. The mean is the mathematical average of a set of two or more numbers.
The mean test score is 85. We will also learn how to solve word problems involving mean. More statistics lessons in this lesson we will learn how to find the mean of a given data set. Arithmetic mean for ungrouped data if n numbers x1x2xn then their arithmetic mean or their average.
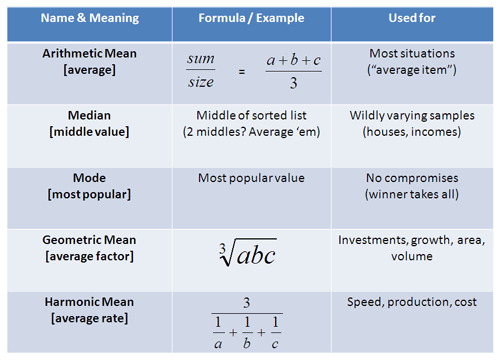
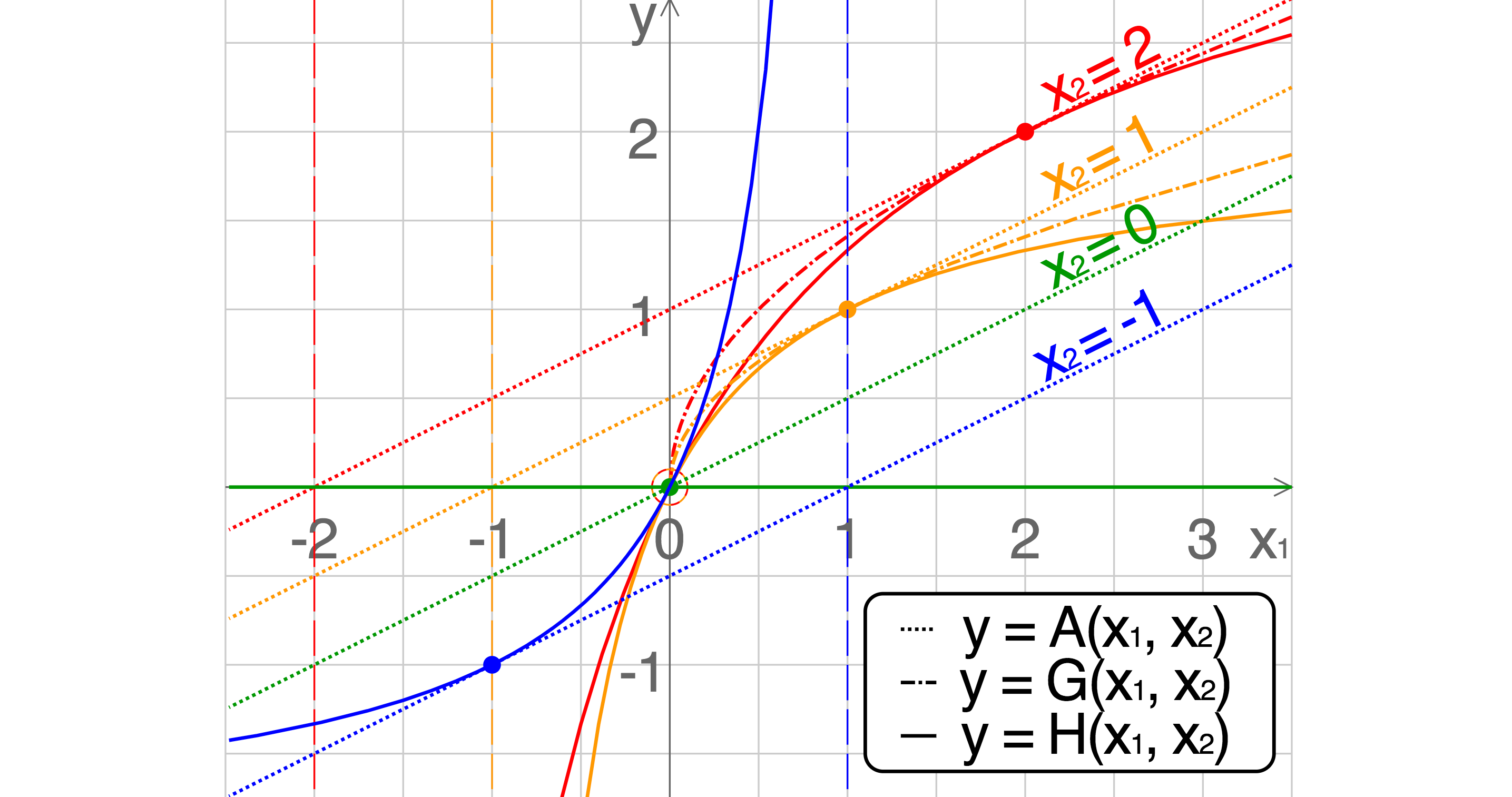
The arithmetic mean is the average of a group of numbers and is computed by summing all numbers and dividing by the number of numbers. The arithmetic mean and the geometric mean are two types of mean that can be calculated. 234566 mean 2345666 266 133. This is not always the case.
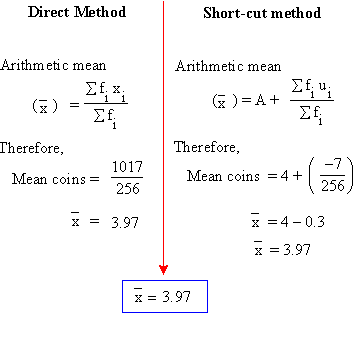
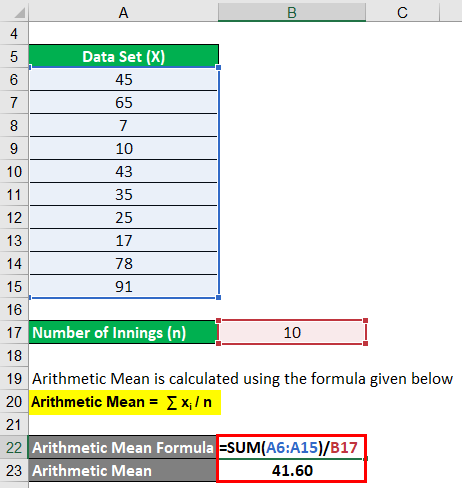
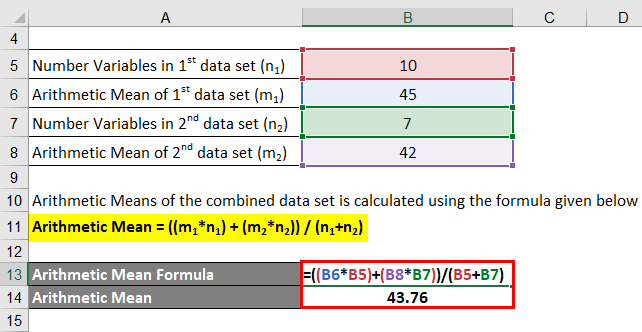
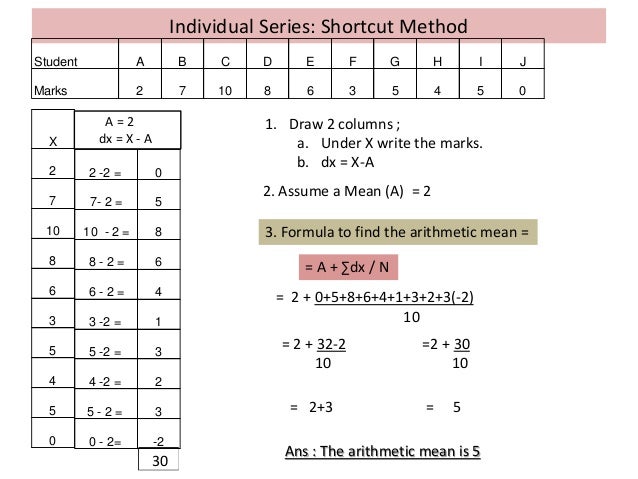
Arithmetic mean formula sum of all of the numbers of a group when divided by the number of items in that list is known as the arithmetic mean or mean of the group. Each formula links to a web page that explains how to use the formula. The greek letter mu is the symbol for the population mean and overlinex is the symbol for the sample mean. In direct method the arithmetic mean is calculated by the following formula.
More statistics lessons calculating mean center of a distribution. Here are the formulas for a population mean and the sample mean. For example the mean of the numbers 5 7 9 is 4 since 579 21 and 21 divided by 3 there are three numbers is 7. A mean is commonly referred to as an average.
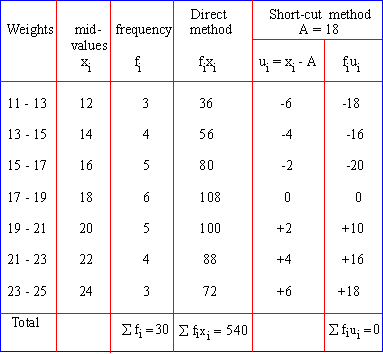
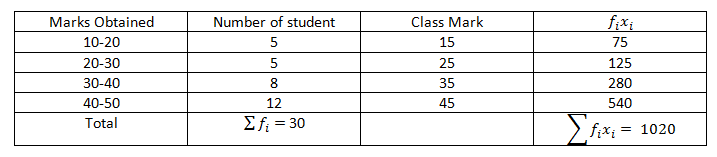
Calculate the mean of the data. It is obtained by dividing the sum of data by the number of observations. Population standard deviation s sqrt s x i m 2 n. The above formula shows that the sum of product of frequencies with their respective variables sfx is to be divided by the sum of the frequencies sf to derive arithmetic mean.
The arithmetic mean of a set of data is found by taking the sum of the data and then dividing the sum by the total number of values in the set. Find the mean of the following set of. Where n is total number of observations. Population mean m s x i n.
But logically both mean and average is same. Let us look into an example to understand this clearly example. The arithmetic mean is also usually just called the mean. The arithmetic mean is the amount secured by dividing the sum of values of the items in a series by the number.
The mean of a set of observations is the average. The mean of the data given above is.











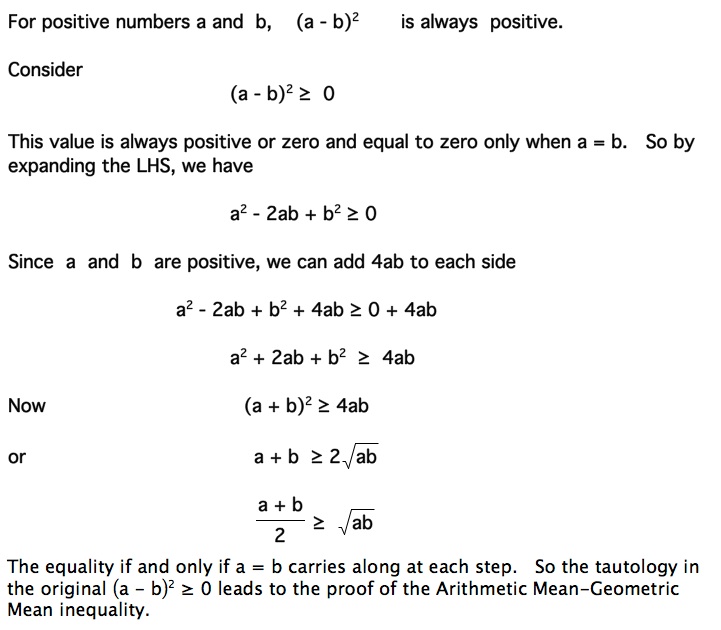



_1499158291_14619-1.jpg)















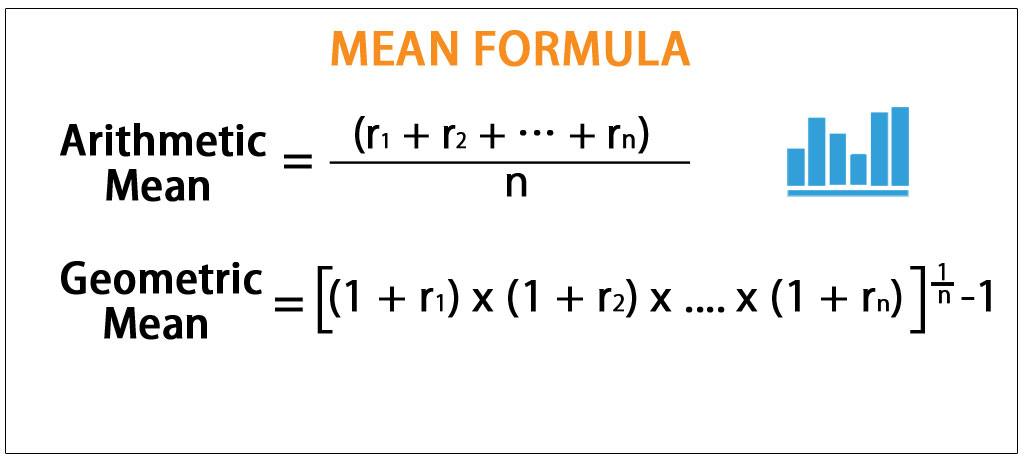





.gif)